Heterodyne detection (also called coherent detection) is a detection method which was originally developed in the field of radio waves and microwaves. There, a weak input signal is mixed with some strong "local oscillator" wave in some nonlinear device such as a rectifier, and the resulting mixing product is then detected, often after filtering out the original signal and the local oscillator frequency. The frequency of the mixing product is the sum or the difference of the frequencies of the signal and the local oscillator.

Figure 1: Setup for optical heterodyne detection.
The resulting photocurrent is proportional to the total optical intensity, thus to the square of the total electric field amplitude. If the signal and local oscillator powers and frequencies are constant, the photocurrent has two different frequency components:
- The constant (zero-frequency) part is proportional to the sum of local oscillator and signal power.
- The part oscillating with the difference frequency (the beat note) has an amplitude proportional to the product of the electric field amplitudes of signal and local oscillator.
With a strong local oscillator, the heterodyne signal resulting from a weak input signal can be much more powerful than for direct detection. In this sense, heterodyne detection provides a signal gain, although there is no optical amplification involved.
Noise Limitations
The noise in the detected signal has different contributions:- There is shot noise, the power spectral density (PSD) of which is proportional to the optical average power.
- The photodetector may add some noise, for example due to some dark current.
- Additional noise can be added by the electronics.
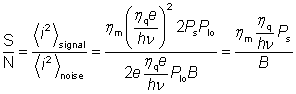
Further increases of local oscillator power would not increase the signal-to-noise ratio, as the signal power and the shot noise PSD are equally increased.
It is also apparent that the beam combiner (see Figure 1) should have a high transmission, so that most of the signal power is sent to the detector. The resulting high loss of local oscillator power at the detector can be compensated by increasing the local oscillator power incident on the beam splitter.
If the beam combiner's transmission is high and the beam overlap is good (ηq ∼ 1), the obtained signal-to-noise ratio is twice that for direct detection. In practice, heterodyne detection can offer a much greater advantage in terms of sensitivity, because direct detection reaches the shot noise limit only for rather high signal powers, whereas with heterodyne detection the standard quantum limit can be reached for much lower signal powers. Note, however, that there are cases where the standard quantum limit can not be reached because detector saturation limits the local oscillator power.
An important detail is that the measured signal is not at zero frequency, but rather at some finite difference frequency, where the detector noise (e.g., 1 / f noise) can be much weaker than around zero frequency.
Using an amplitude-squeezed local oscillator beam, it is even possible to beat the standard quantum limit with heterodyne detection.
Spatial Single-mode Nature of Heterodyne Detection
A strong heterodyne signal is obtained only if the beam overlap factor ηm is high. If the local oscillator beam is a perfect Gaussian beam, one may consider the total incident input signal light as a superposition of modes, using the mode system which is defined by the local oscillator beam. We see then that only the signal light in the lowest-order mode (the Gaussian) contributes to the heterodyne signal, because the overlap factors are zero for all higher-order modes. For any such higher-order mode, interference still occurs on the photodiode, but the local oscillations of intensity cancel out by integrating the power over the full detector area, provided that the detection efficiency is uniform over the full beam area.The single-mode nature of heterodyne detection is a crucial aspect. It can be very helpful, for example by suppressing influences of stray light in sensitive measurements. On the other hand, it would greatly reduce the detection efficiency, for example when light scattered on a large area needs to be detected.
In principle, one could use a local oscillator beam consisting of different spatial modes, ideally each one being associated with a separate optical frequency. That would allow to simultaneously and independently measure signals in multiple modes. However, the power of each signal component in the heterodyne signal would then be proportional to the local oscillator power in the corresponding mode, whereas the noise level would be determined by the total local oscillator power. This shows again that heterodyne detection is essentially a single-mode detection technique.
Balanced Detection

Figure 2: Setup for balanced optical heterodyne detection.
Temporal Coherence Issues
If the laser delivering the local oscillator beam is totally independent of the signal, it is hardly possible to measure the phase of the input signal, because the phase of the electronic signal is also dependent on the local oscillator phase, which is stable only over the typically short coherence time.If phase measurements are required, the local oscillator and signal waves are usually generated from a single source, so that the relative phase of the two beams is fairly stable even if the source does not exhibit particularly low phase noise. For example, a signal wave may be generated from a local oscillator wave by frequency-shifting part of it with an acousto-optic modulator. A heterodyne measurement can then very sensitively reveal any phase changes to that signal.
By bandpass-filtering the electronic signal, it is also possible to sample a very narrow spectral portion of the signal. That detection bandwidth can easily be far below what is possible with optical bandpass filters. This can be useful for precision spectroscopy, for example.
Homodyne Detection
A variant of heterodyne detection is homodyne detection, where the local oscillator frequency equals the signal frequency. For optical homodyne measurements, both waves are virtually always derived from the same laser source. The homodyne technique is phase-sensitive in the sense that the power of the heterodyne signal depends on the relative phase of signal and local oscillator, and may even totally vanish.A useful modification is balanced homodyne detection, where two photodiodes (Figure 2) are used after a beam splitter with precisely 50% reflectivity, and the sum and difference of photocurrents are electronically obtained. If the signal port is blocked, the difference of photocurrents exhibits the shot noise level of the local oscillator beam, even if the actual noise level of that beam is different. The latter noise level can be obtained in addition by taking the sum of the photocurrents. That sum exhibits the same noise as for direct detection of the local oscillator beam with a single photodiode. The homodyne setup provides the difference signal in addition, which allows one to conveniently compare the actual noise with the shot noise limit. For amplitude-squeezed light, the sum of the photocurrents exhibits a lower noise than the difference. In many squeezed-light experiments, the degree of squeezing is measured with the homodyne technique.
A possible interpretation of the situation without signal input is that the setup then measures vacuum noise. This is because although no photons can enter the signal input port, there are still vacuum fluctuations of the electric field. The measured local oscillator shot noise is interpreted as being caused not by the local oscillator beam, but rather by the vacuum noise [5]. This interpretation is supported by the fact that amplitude-squeezed light at the signal input can reduce that noise level. These findings are in conflict with the earlier (and still widespread) idea that shot noise is intrinsic to the detection process rather than a property of the light field.
Heterodyne Measurements with Pulsed Beams
The heterodyne technique can also be applied to pulsed signals by using a pulsed local oscillator beam. It is even possible to use ultrashort pulses. As the heterodyne detector is essentially sensitive only while the local oscillator light is there (assuming a signal power well below the local oscillator power), it is possible to obtain a very high temporal resolution without requiring a very fast photodetector. This technique is called heterodyne (or homodyne) linear optical sampling.Applications of Heterodyne Detection
Some examples for the application of optical heterodyne detection are:- Heterodyne detection is used for coherent Doppler LIDAR measurements (and related laser radar techniques), where very weak light scattered in the atmosphere needs to be detected. It is possible, for example, to accurately measure wind speeds based on the Doppler shift. By deriving the signal and local oscillator beams from the same laser source (see above), it is possible to resolve very small Doppler shifts.
- There are other applications in spectroscopy. Examples are solar radiometry [3] and cavity ring-down spectroscopy [13].
- The linewidth of a laser, for example, can be measured with the self-heterodyne technique, where a frequency-shifted copy of the laser beam is superimposed with a temporally delayed copy on a photodetector.
- In optical fiber communications, the phase sensitivity of heterodyne and homodyne detection allows one to demodulate phase-encoded signals [7, 9], based on techniques like frequency shift keying (FSK) (→ coherent communications). Also, it the basis for some forms of electronic dispersion compensation.
Ricardo Monroy C.I. 17646658