GEOMETRÍA DE LA FIBRA MICRO-ESTRUCTURADA

La fibra micro-estructurada consta de un medio homogéneo de Sílice de alta pureza con un arreglo hexagonal de huecos de aire, de diámetros d diferentes y distancia L entre huecos consecutivos, dispuestos en siete anillos hexagonales que se mantienen a lo largo de la estructura, ver Figuras 3.

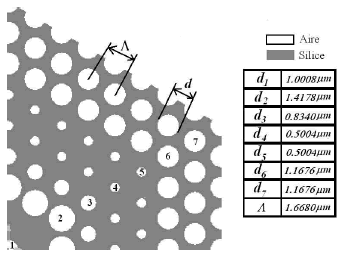
Figura 3. Un cuarto de la fibra con los diámetros de los huecos de aire, donde los números representan los diferentes diámetros
Figure 3. One quarter of the fiber with the air-holes diameters, where the numbers represent the different diameters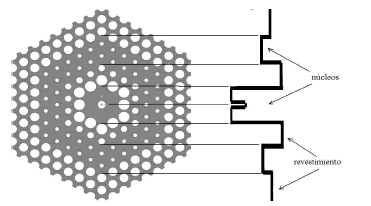

La Figura 4 muestra la estructura junto a su perfil de índice de refracción, donde se puede identificar claramente dos regiones de mayor valor del índice de refracción que actuarían como núcleos, y las demás que son menor harían de revestimiento. Nótese que el primer anillo de huecos se ha desaparecido para así obtener una región central de 4L de diámetro que actúa como núcleo.

Figura 4. La estructura completa con su perfil de índice de refracción
Figure 4. Complete structure joins at its refraction index profile

debido a la doble simetría que presenta la fibra, tal como se muestra en la Figura 5(a), usando elementos triangulares de primer orden. El discretizado fue refinado en la región que contiene los dos núcleos, porque allí es donde se confina fuertemente el campo eléctrico (Figura 5b).

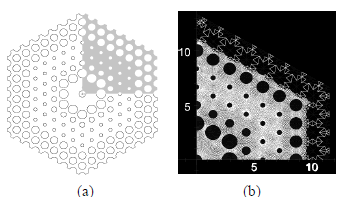
Figura 5. Discretización de un cuarto de la sección transversal de la fibra
Figure 5. One quarter discretization of the fiber cross section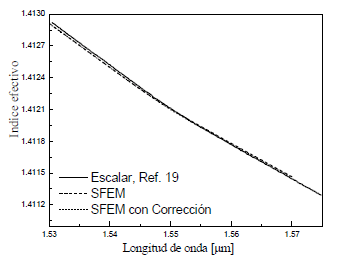

En las Figuras 6 y 7 se comparan los resultados obtenidos del índice efectivo y el parámetro de dispersión del modo fundamental tipo HE₁₁ con el análisis escalar reportado en [19], sobre un rango de longitud de onda desde 1.530 mm a 1.575 mm. La curva sólida representa el análisis escalar de la Ref. 19, la curva segmentada es nuestro análisis escalar y la curva punteada es nuestro análisis teniendo en cuenta la corrección por efectos de polarización.

Figura 6. Curva del índice efectivo en función de la longitud de onda
Figure 6. Effective index curve as wavelength function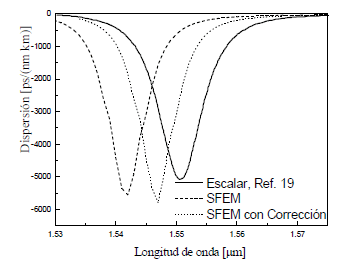

Figura 7. Curva del parámetro de dispersión en función de la longitud de onda
Figure 7. Dispersion parameter curve as wavelength function

Nótese que en esta estructura, la luz se propaga en la parte central y en la región que tiene los huecos de aire más pequeños (ver Figura 8), por lo que el acople entre las componentes ortogonales del campo eléctrico es relativamente fuerte y, por consiguiente, el resultado de las soluciones escalares para el índice efectivo y la dispersión difieren de la solución que incluye la corrección por efectos de polarización como se muestra en las figuras 6 y 7.

Figura 8. Perfil de intensidad del campo eléctrico para el modo tipo HE₁₁ calculado con SFEM para las longitudes de onda: (a) l=1.530 mm, (b) l=1.547 mm, (c) l=1.570 mm
Figure 8. Electric field intensity profile for HE₁₁-like mode is computed with SFEM to wavelengths: (a) l=1.530 mm, (b) l=1.547 mm, (c) l=1.570 mm

El análisis muestra que para longitudes de onda inferiores a 1.547 mm la luz está mayoritariamente confinada en el núcleo central y la dispersión es muy pequeña (ver Figuras 7 y 8a), mientras que para longitudes de onda superiores la luz se encuentra mayoritariamente confinada en el núcleo externo y la dispersión también es pequeña (ver Figuras 7 y 8c). En cambio, justo en la longitud de onda de 1.547 mm el índice efectivo cambia drásticamente su pendiente (ver Figura 6) y, por ende, se produce un gran pico de dispersión anómala de aproximadamente -5800 ps/(nm-km) y allí la luz esta confinada en ambos núcleos con igual intensidad (ver Figuras 7 y 8b). Debido a este pico de dispersión anómala es que esta fibra tiene un gran potencial como compensadora de dispersión normal.


Ricardo Monroy    C.I.17646658