Óptica de Fourier

La óptica de Fourier es una rama de la teoría óptica ondulatoria, basada en los descubrimientos del físico y matemático francés Joseph Fourier, concretamente en la Transformada de Fourier. Es una de las tres principales aproximaciones al estudio de la óptica, siendo las otras la integral de difracción y la óptica geométrica. Es válida en el ámbito de la óptica lineal, esto es, siempre que consideremos lineales los sistemas estudiados.
Básicamente considera un haz de luz en un plano del espacio como una distribución de luz, pero también como una distribución de luz sobre el plano transformado de Fourier, donde cada punto corresponde no a un lugar en el espacio sino a una frecuencia espacial. De este modo las frecuencias espaciales caracterizan la variación de distribución de la luz sobre la superficie y toman el valor del número de ondas.
La principal ventaja de este enfoque es la equivalencia entre las operaciones de transferencia de un sistema en el dominio del espacio o en el de las frecuencias espaciales. La convergencia de ambas funciones (la de distribución de la luz y la de transferencia del sistema) en el dominio del espacio resulta en un simple producto de las transformadas de Fourier el dominio de las frecuencias espaciales.
Desde este modo, obteniendo la función de transferencia y la correspondiente transformada de Fourier para cada sistema óptico se simplifica enormemente el problema de la propagación de la luz en el espacio, obteniendo así una importante herramienta para el tratamiento espacial de situaciones complejas aprovechando todo el desarrollo de la teoría de la transformada de Fourier en otros ámbitos de la ciencia.
Su aplicación más directa es el filtrado espacial de imágenes, en el que mediante operaciones sencillas sobre el plano transformado (aquel en el que aparece la transformada de Fourier de distribución de la luz y que se puede obtener físicamente por ejemplo con una lente) permite manipular la luz, por ejemplo suprimiendo las frecuencias especiales del plano transformado para obtener modificaciones sobre la imagen. Si se suprime por ejemplo la frecuencia cero, que aparece en el centro del plano transformado se elimina la luz de fondo, mientras que si se eliminan las frecuencias altas se suavizan las formas de los objetos.
Esto tiene aplicaciones en todos los ámbitos donde se empleen haces de luz, especialmente luz láser: comunicaciones ópticas, holografía y computación óptica, e incluso simulando los fenómenos ópticos se puede emplear para el tratamiento informático de las imágenes

El modelo ondulatorio de la luz es el que mas se adecua al estudio de la óptica no cuántica y es el único utilizado para el tratamiento de fenómenos como los de difracción, interferencia y polarización. En gran parte de la literatura dedicada a la enseñanza de la Física general y experimental, al llegar al estudio de la óptica geométrica suele presentarse una ruptura en el desarrollo del discurso como si se tratara de un tema que prácticamente no está relacionado con el resto de la disciplina en cuestión.

Por otra parte, en cursos mas avanzados, se hace un paso a la óptica geométrica a partir del modelo ondulatorio acudiendo mayormente al concepto, pero suele llegarse a ésta sin utilizarla para establecer algo que muestre explícitamente que se ha entrado en tópicos tratables por la ley de Sneel o al menos por el Principio de Fermat, dejando insatisfecho al estudioso que tiene por óptica geométrica la aplicación de las citadas formulaciones.
También se presenta la situación de que el estudiante interesado, encuentra en los medios, alusiones a temas como el procesamiento de imágenes, escucha hablar de wavelets, de uso de la transformada de Fourier en óptica, etc., sin que advierta vínculo alguno con lo que ha aprendido en sus estudios regulares. Y se da muy frecuentemente que oftalmólogos y optometristas reciben literatura especializada en la que encuentran referencias a aplicaciones de la Óptica de Fourier en oftalmología y optometría, sin que encuentren apropiados textos sobre esos temas en los que puedan ahondar sobre los mismos.
Tratando de atender aunque sea en forma lo mas elemental posible, al saludable interés intelectual al que nos hemos referido, se ha elaborado el presente trabajo.
En la Óptica de Fourier se estudian fenómenos de las ondas electromagnéticas y por tanto de las luminosas, haciendo un uso fundamental de la teoría de la Transformada de Fourier.
La transformada de Fourier es una aplicación que hace corresponder a una función f(x) de valores complejos de x.
Veamos una aplicación al estudio de la intensidad luminosa en el patrón obtenido en la difracción de Fraunhofer. Para obtenerlo se hace incidir un haz paralelo de luz en una pantalla opaca con un hendidura muy fina la cual difracta la luz que después de ser refractada por una lente convergente forma el patrón en un plano situado a la distancia focal f de la lente llamado plano de Fourier. La intensidad luminosa I(x´,y´) viene dada por el cuadrado de la transformada de Fourier de la función de transmisión t(x,y) de la hendidura:

Donde x´ e y´, coordenadas en plano de Fourier de los puntos que conforman el patrón los cuales son funciones de las frecuencias espaciales y de la longitud de onda (siendo
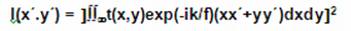
k=2) La trasformada inversa de Fourier de la correspondiente a la formación del patrón, producida por una segunda lente convergente, corresponderá a la de la formación de la imagen definitiva.
La óptica geométrica muestra que f, distancia focal de la lente convergente y las distancias s objeto-lente y s´ lente –imagen están relacionadas por la fórmula de Descartes.
1/s+1/s´=1/f en cuya aplicación no se tiene en cuenta para nada la formación del patrón en el plano de Fourier. No fue hasta finales del siglo XIX y principios del XX que Abbe y Porter descubren la intervención del patrón en la formación de la imagen final al aplicarse el principio de Huygens- Fresnel en el proceso. La aplicación de la teoría de Abbe-Porter y la Óptica de Fourier ha permitido implementar métodos de filtrado de frecuencias en el plano de Fourier, colocando en el mismo dispositivos como rejillas que eliminen frecuencias perturbadoras de la calidad de la imagen. Las posibilidades de la computación y los avances teóricos de la "Óptica de Fourier, de los procedimientos basados en las wavelets, de los fractales, etc. han propiciado un notable progreso en el campo del tratamiento de imágenes.
El otro punto que vamos a tratar, como indicamos en el comienzo de este trabajo, se refiere a la introducción de la formulación propia de la óptica geométrica a partir de la óptica ondulatoria. Para ello, partiremos de la ecuación de las ondas electromagnéticas puesto que electromagnética es la naturaleza de la luz:



Con las suposiciones que en aras del mejor entendimiento hemos realizado faltando un tanto al rigor pero no a la descripción física, podemos observar que r nos señala dirección del rayo perpendicular a la fase que es como decir a la superficie de onda dada por la función escalar L, de manera que el gradiente de esa función (L, nos dará el desplazamiento en la dirección del rayo, de la superficie de onda..
Se cumplirá pues que:


Volvamos a la ecuación de la iconal. Para el caso de de una propagación del rayo según el eje X o sea para (valiendo cero grados y ( noventa, con x como única componente de r, se tendrá que por la ecuación de la iconal:

expresión del camino óptico para un caso particular que nos permitirá didácticamente en lo que sigue aplicar el Principio de Fermat a la deducción de la ley de Snell y evidenciar la formulación de la óptica geométrica partiendo de la óptica ondulatoria.


Ricardo Monroy      C.I. 17646658

---